نظریه توازن اولین بار توسط هایدر[1] در سال 1958 مطرح شد، میتوان در چارچوب این نظریه به مثلثهای تشکیل شده در یک شبکه بسته به وزن یالهای آن، انرژی نسبت داد. ایده نظریه توازن این است که برای یک جامعه که متشکل از افراد و روابط بین آنها است اگر به کوچکترین گروهها که افراد در آنان میتوانند به طور مستقیم و غیر مستقیم بر یکدیگر اثر بگذارند توجه کنیم با گروههایی 3 نفره مواجه میشویم که روابط بین آنها میتوانند دوستی و یا دشمنی باشد. بنابراین در یک جمع سه نفره، 4 حالت از روابط وجود دارد.
1- حالت نخست آن است که هر سه نفر دوست یکدیگر باشند. در این مثلث از روابط همه چیز خوب است! هر دو نفر دوست یکدیگر هستند و این جمع از لحاظ اجتماعی پایدار است. بنابراین به این مثلث یک مثلث متوازن گفته میشود. یالی که دوستی را نشان دهد، وزن مثبت دارد و یالی که دشمنی را نشان دهد وزنش منفی است. در این حالت هر سه یال وزنشان مثبت است.
2- حالت دوم آن است که هر سه نفر دشمن یکدیگر باشند! آنگاه هر لحظه ممکن است درگیری بین اعضا پیش آید و گروه دچار تغییر در وضعیت خود شود. بنابراین هایدر این مثلثها را مثلثهای نامتوازن نامید.
3- حالت دیگر آن است که در مثلث، یک دشمن مشترک وجود داشته باشد. یعنی بین دو نفر رابطه دوستی و بین آن دو نفر و شخص سوم رابطه دشمنی وجو داشته باشد. این مثلث متوازن است. با اینکه پایداری وضعیت این مثلث به اندازه حالت اول نیست ولی از آنجا که دشمن مشترک وجود دارد، این مثلث از روابط تمایلی به تغییر وضعیت خود ندارد چرا که هر تغییر رابطه سبب قرار گرفتن در حالت بدتری میشود.
4- حالت آخر، وضعیتی است که فقط یکی از روابط دشمنی باشد. این شبکه نامتوازن است. سهتایی را فرض کنید که مردی همسرش و مادرش را دوست دارد ولی مادر و همسرش با یکدیگر رابطه حسنهای ندارند. این مثلث به وضوح نامتوازن است چرا که در این وضعیت فشاری بر روابط وجود دارد که برای متوازن شدن این سهتایی یا باید رابطه مادر و همسر (عروس خانواده) به دوستی تبدیل شود و سهتایی به حالت 1 برود یا اینکه مرد قید مادر یا همسرش را بزند و سهتایی را به حالت 3 تبدیل کند.
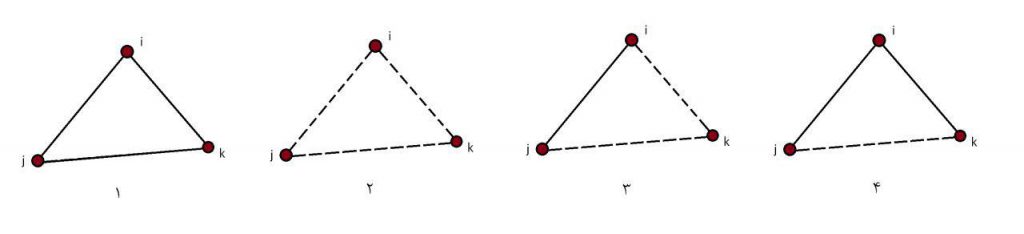
حالتهای مختلف روابط سهتایی. خط ممتد به معنی دوستی بین دو نفر و خط چین به معنای دشمنی بین دو نفر است. مثلثهای 1 و 3 ، مثلثهای متوازن و مثلثهای 2 و 4 مثلثهای نامتوازن هستند.
در ادامه مارول و استروگتز با ایده گرفتن از مسئله پایداری در سیستمهای فیزیکی، به این مثلثها انرژی نسبت دادند[2] به این صورت که قرینه حاصل ضرب یالهای مثلث را به عنوان انرژی آن مثلث معرفی کردند. به این صورت که برای مثلثی با رئوس i, j, k انرژی آن برابر است با:
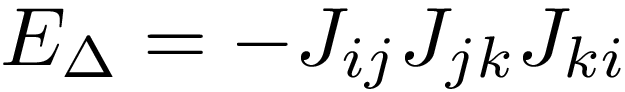
طبق این تعریف، مثلثهای متوازن دارای انرژی منفی و مثلثهای نامتوازن دارای انرژی مثبت هستند. در فیزیک معمولا پایداری یک سیستم در انرژیهای کمتر، بیشتر است. بنابراین میتوانیم با دانستن وزنهای یک شبکه، انرژی مثلثهای تشکیل شده در شبکه را بهدست آوریم و سپس با جمع زدن روی همه مثلثها میتوانیم انرژی کل شبکه را بهدست آوریم.
انتظار داریم که سیستم تمایل داشته باشد از انرژی بیشتر به انرژی کمتر برود. به عنوان مثال اگر مثلثی در حالت 2 یا 4 باشد تمایل دارد به سمت حالت 1 یا 3 برود. مثال زیر را در نظر بگیرید:
فرض کنید که شما با زوجی دوست هستید که از هم جدا میشوند در این صورت شما دو روش برای برخورد با این وضعیت دارید، 1) اینکه سعی کنید به دوستی خود با هر دو نفر ادامه دهید و 2) اینکه روابط خود را با یکی از طرفین قطع کنید. اگر راه اول را انتخاب کنید در وضعیتی قرار میگیرید که باید مدام به شکایتهای هر دو در مورد یکدیگر گوش دهید بنابراین در نهایت مجبور میشوید که رابطه خود با یکی از طرفین را قطع کنید.
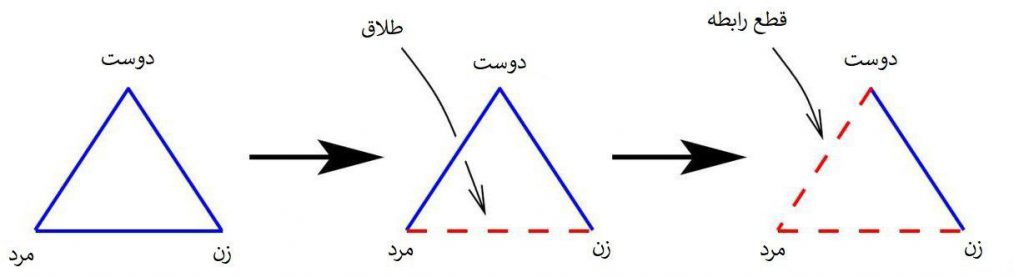
دینامیک تحول مثلث از روابط هنگامی که در حالت نامتوازن قرار گیرد. دینامیک مثلث از عدم توازن به سمت توازن است[3]
دینامیک شبکه:
در سالهای اخیر بحث دینامیک شبکهها و رفتارهای جمعی که در غالب آن ظهور میکنند، توجه بسیاری از دانشمندان را به خود جلب کرده است. اولین بار آنتال و همکارانش دو مدل برای دینامیک شبکه طبق نظریهی توازن معرفی کردند[3]. طبق این دو مدل تغییرات در شبکه به شرطی رخ میدهند که تنش در شبکه کاهش یابد. بر این اساس آنتال یک انرژی پتانسیل برای شبکه تعریف میکند که شبیه به آنچه بالاتر گفته شد قرینه حاصل جمع انرژی تک تک مثلثهای موجود در شبکه است باین تفاوت که مقدار این انرژی بر تعداد کل مثلثهای موجود در شبکه تقسیم میشود تا مقداری بین 1 و 1- داشته باشد. که این پتانسیل را در ادامه مشاهده میکنید.
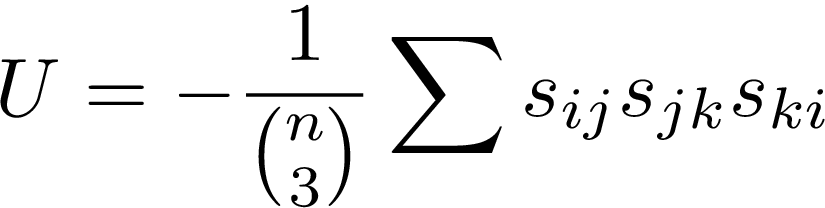
این رابطه همارز با رابطه زیر است:
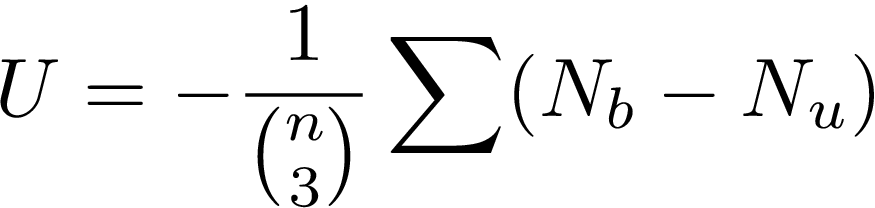
![]() و
و ![]() به ترتیب تعداد مثلثهای متوازن و نامتوازن داخل شبکه را نشان میدهند. در ادامه دینامیکهایی که آنتال برای تغییر علامت پیوندها در یک شبکهی نامتوازن جهت رسیدن به حالت متوازن را پیشنهاد کرده معرفی میکنیم.
به ترتیب تعداد مثلثهای متوازن و نامتوازن داخل شبکه را نشان میدهند. در ادامه دینامیکهایی که آنتال برای تغییر علامت پیوندها در یک شبکهی نامتوازن جهت رسیدن به حالت متوازن را پیشنهاد کرده معرفی میکنیم.
به طور کلی با دو رویکرد مختلف میتوان دینامیک این شبکهها ( شبکههای کاملا همبند) را تعریف کرد؛ رویکرد اول این است که تغییرات تنها با در نظر گرفتن شرایط موضعی صورت گیرد مثلا برای بررسی امکان تغییر وزن یک یال تنها تفاوت وضعیت دو راس این یال بعد و قبل از تغییر مد نظر قرار گیرد یا اینکه امکان تغییر تنها بین سه راس خاص بررسی شود. اما رویکرد دوم برخلاف رویکرد اول به حالت کلی سیستم توجه دارد یعنی تغییر یک یال اگر انرژی کل سیستم را کمتر کند میتواند انجام شود.
یک نوع دینامیک موضعی، دینامیک موضعی سهتایی است به این شکل که یک مثلث نامتوازن به طور تصادفی انتخاب میشود و با تغییر یکی از یالها به توازن میرسد، و این تغییر بدون توجه به شکل تغییرات در حالت کلی سیستم رخ میدهد. ![]() را به عنوان مثلثی با n یال (-) تعریف میکنیم یعنی
را به عنوان مثلثی با n یال (-) تعریف میکنیم یعنی ![]() یک مثلث با ۳ یال منفی و
یک مثلث با ۳ یال منفی و ![]() یک مثلث با ۱ یال منفی و ۲ یال مثبت است و با تعریفی که هایدر از یک مثلث متوازن ارائه داده بود
یک مثلث با ۱ یال منفی و ۲ یال مثبت است و با تعریفی که هایدر از یک مثلث متوازن ارائه داده بود ![]() و
و ![]() مثلثهای متوازن و
مثلثهای متوازن و ![]() و
و ![]() مثلثهای نامتوازن هستند. با این تعاریف دینامیک موضعی مثلثها شامل سه قدم زیر میشود:
مثلثهای نامتوازن هستند. با این تعاریف دینامیک موضعی مثلثها شامل سه قدم زیر میشود:
1- انتخاب تصادفی یک مثلث نامتوازن
2- اگر مثلث انتخاب شده ![]() بود با احتمال
بود با احتمال ![]() یال منفی را به یال مثبت تغییر میدهیم و یا با احتمال
یال منفی را به یال مثبت تغییر میدهیم و یا با احتمال ![]() یکی از یالهای مثبت را به منفی تغییر میدهیم.
یکی از یالهای مثبت را به منفی تغییر میدهیم.
3- اگر مثلث ![]() بود یک یال را به طور تصادفی انتخاب میکنیم و علامتش را از منفی به مثبت تغییر میدهیم.
بود یک یال را به طور تصادفی انتخاب میکنیم و علامتش را از منفی به مثبت تغییر میدهیم.
به این شکل یک مثلث نامتوازن به مثلث متوازن تبدیل میشود هر چند ممکن است در این تغییر مثلث متوازن دیگری نامتوازن گردد یا حتی انرژی کل سیستم افزایش یابد. این نوع دینامک را LTD یا دینامیک سهتایی محلی مینامند.
سه قدم بالا کل فرایند لازم برای دینامیک موضعی مثلثها میباشد، حالا نتایج تحول یک شبکه کامل (همبند) با N راس را تحت این دینامیک نشان میدهیم. نتایج نشان میدهند که با تعریف پارامتری به نام چگالی یالها و بررسی این پارامتر طی فرآیند تحول اگر چگالی یالهای دوستی در ابتدا بیشتر از 0.5 باشد در نهایت تمام اعضای شبکه با یکدیگر رابطهی دوستی خواهند داشت که به این حالت بهشت میگویند، اما در غیر اینصورت اعضای شبکه به دو دسته تقسیم میشوند که در درون هرکدام اعضا با هم رابطه دوستی دارند ولی روابط بین دو دسته، همه دشمنی است که به این حالت دوقطبی میگویند.
اما نوع دوم دینامیکهای قابل تعریف برای شبکههای متوازن همانطور که گفته شد به حالت کلی سیستم توجه دارد، یعنی در هر قدم زمانی، تحولات طوری انجام میشوند که تنش در کل سیستم کاهش یابد و به عبارت دیگر انرژی کل سیستم پایین آید. یکی از دینامیکهای قابل تعریف از این جنس، دینامیک CTD یا دینامیک سهتایی مقید میباشد. که به این شکل تعریف میشود:
یک یال تنها به شرطی تغییر میکند که این تغییر، انرژی کل شبکه را کاهش دهد.[3]
معنای این جمله آن است که اگر تعداد مثلثهای نامتوازنی که یک یال در آن وجود دارد از تعداد مثلثهای متوازن که همان یال در آنها وجود دارد بیشتر بودند، علامت یال تغییر میکند تا تعداد مثلثهای متوازن در کل شبکه افزایش و انرژی کل شبکه کاهش یابد.
کمینههای محلی:
حالتهای شبه پایدار، حالتهای مسدود یا کمینههای محلی همانطور که قبلا هم گفته شد زمانی اتفاق میافتند که سیستم در روند تحول خود در یک حالت مسدود خاص گیر بیفتد و دیگر به حالت تعادل نهایی خود نرسد. مطالعات نشان دادهاند که شبکههای کوچک کمینه محلی یا حالت مسدود ندارند و حالتهای مسدود وقتی اتفاق میافتند که تعداد راسهای یک شبکه 6 یا 8 یا 9 و یا بیشتر از 11 راس باشند.[2]
برای روشن تر شدن موضوع لازم است که ابتدا مفهوم حالتهای همسایگی را توضیح دهیم: دو پیکربندی زمانی همسایه هستند که بتوان از یکی با تغییر علامت یال به دیگری رسید. بنابراین تعریف، یک حالت مسدود که اولین بار توسط آنتال [3]تعریف شد، پیکربندیای است که از تمام پیکربندیهای همسایهی خود انرژی بالاتری دارد. مطالعات بعدی که توسط مارول و استروگتس و با استفاده از دستهی خاصی از گرافها به نام گرافهای “پالی” و نتیجهی سایدل برای دو گراف انجام شد، نشان داد که حالتهای مسدود با انرژی بالا (عددی نزدیک صفر) نه تنها نادرند بلکه ثابت شد که مقدار عددی انرژی این حالات بیشتر از صفر نخواهد بود.[2] در شکل زیر نمونههایی از پیکربندیهای همسایگی را برای شبکههایی با سه و چهار راس مشاهده میکنید.
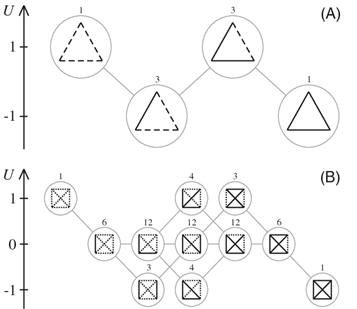
شکلهای A و B به ترتیب حالتهای همسایگی را برای گرافهایی با 3 و 4 راس نشان میدهند.[2]
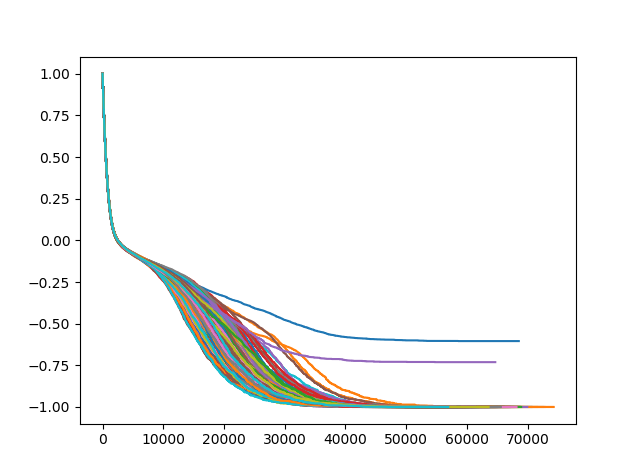
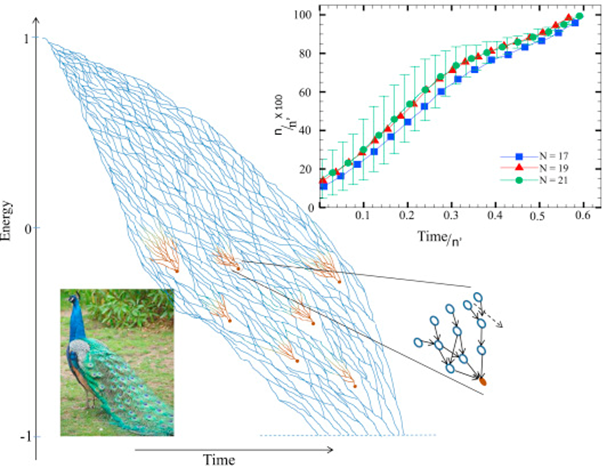
همانطور که قبلا هم گفتیم شبکه به سمت حالتی با تنش کمتر تکامل مییابد، توجه کنید که در آغاز دینامیک شبکه، احتمال کاهش انرژی سیستم با تغییر علامت یک یال زیاد است، اما در همسایگی یک حالت با انرژی کمینه، تعادل نهایی و یا کمینه محلی، یالهای کمتری اجازه دارند در راستای کاهش انرژی تغییر علامت دهند و این به خاطر آن است که یالهای کمتری وجود دارند که با تغییر علامت آنها انرژی سیستم کاهش مییابد. بنابراین مشاهده میکنیم که شکلی مخروطی به سمت کمینه انرژی شکل میگیرد. آنچه گفته شد ثابت شده و این اثبات با استفاده از مفهوم هامیلتونی و مشارکت و با تعریف شاخصی برای مشخص کردن مسیرهای مخروطی که به سمت حالت مسدود حرکت میکنند، انجام شده است[4]. این شاخص “نسبت مشارکت معکوس (IPR)” نام دارد و میزان مشارکت راسها در تحول سیستم را نشان میدهد. مطالعات نشان دادند که حالتهای مسدود را میتوان با بررسی رفتار نسبت مشارکت معکوس (IPR) در کمترین ویژه مقدار یعنی حالتی که مشارکت رئوس در نزدیکی آن افزایش می یابد، تشخیص داد[5]. نسبت مشارکت معکوس را با رابطه ی زیر مشخص میکنند. که این رابطه را در زیر مشاهده میکنید:
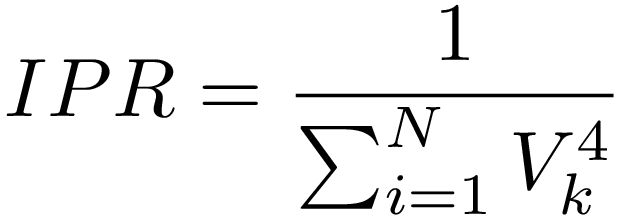
در رابطه ی بالا ![]() ، i امین جزء از بردار ویژهی متناظر با یک مقدار ویژهی مشخص است. در شکل زیر مسیرهای مخروطی به سمت حالات مسدود را مشاهده میکنید که با رنگ قرمز مشخص شدهاند.
، i امین جزء از بردار ویژهی متناظر با یک مقدار ویژهی مشخص است. در شکل زیر مسیرهای مخروطی به سمت حالات مسدود را مشاهده میکنید که با رنگ قرمز مشخص شدهاند.
روشهای تشخیص حالتهای مسدود:
در شبیه سازیها اگر با حالتی مواجهه شویم که حدس میزنیم حالت مسدود است میتوان با ساز وکارهایی تشخیص داد که آیا این حالت واقعا یک حالت مسدود است یا اگر به سیستم زمان بیشتری بدهیم میتوان دید که این حالت به تعادل نهایی همگرا میشود. بهترین روش آن است که ببینیم آیا با تغییر تک تک یالها در شبکه، انرژی شبکه کاهش مییابد یا خیر، که اگر انرژی شبکه کاهش یافت در این صورت این حالت یک حالت مسدود نخواهد بود. همچنین اگر سیستم را از مرتبهی سوم تعداد راسها بررسی کرده باشیم (یعنی فرایند انتخاب یک یال رندم و تغییر آن یال را ![]() بار انجام داده باشیم) میتوان اطمینان داشت که حالت رخ داده، یک حالت مسدود است. روش دیگری که شهودی به ما میدهد استفاده از الگوریتم دندوگرام میباشد.
بار انجام داده باشیم) میتوان اطمینان داشت که حالت رخ داده، یک حالت مسدود است. روش دیگری که شهودی به ما میدهد استفاده از الگوریتم دندوگرام میباشد.
دندوگرام:
یک دندوگرام (در یونانی دندو به معنای “درخت” و گرام به معنای “کشیدن” است) نمایش بصری (درختی) همبستگی دادههای مرکب است. اجزاء یکتا در پایین ترین سطح قرار داده شدهاند و از آنها به عنوان برگ یاد میشود. خوشهها از ترکیب اجزاء یکتا با یکدیگر و یا ترکیب خوشههای موجود با یکدیگر به دست میآیند و به نقطهی پیوستن آنها راس میگویند. در هر راس یک زیر شاخهی راست و یک زیر شاخهی چپ از خوشهها و یا اجزا یکتا داریم. از دندوگرامها اغلب در زیست شناسی محاسباتی برای نشان دادن خوشهبندی ژنها یا نمونهها و یا در دستگاههای حرارتی استفاده میشود. در شکل زیر نمونهای از یک دندوگرام را مشاهده میکنید.
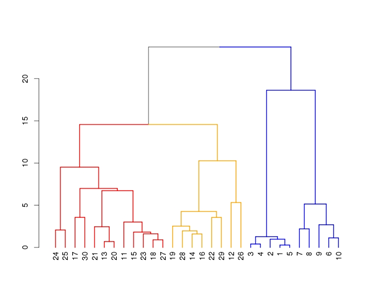
دندوگرام نشان میدهد که چگونه هر خوشه با کشیدن یک پیوند U شکل بین یک خوشه غیر تکین و فرزندانش شکل میگیرد. راس نشان میدهد که دو خوشه ترکیب شدهاند. طول دو پایه U-link نشان دهنده فاصله بین خوشههای فرزند است. به بیان دیگر یک دندوگرام، گرافی با ساختار درختی است که در نقشههای گرمایی استفاده میشود تا نتیجه یک خوشهبندی سلسله مراتبی را نشان دهد. نتیجه خوشهبندی یا به صورت فاصله و یا به صورت شباهت سطرها و یا ستونهای خوشهای نشان داده میشود که وابسته به واحد اندازهگیری فاصله است. در ادامه دو مورد از این واحدها را توضیح میدهیم.
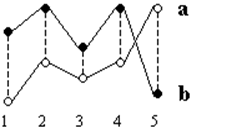
فاصله اقلیدسی: فاصله اقلیدسی بین دو نقطه a و b و بعد k به صورت زیر محاسبه میشود. توجه کنید که در خوشه بندی بعد به معنای تعداد متغیرها در هر سطر یا ستون میباشد.
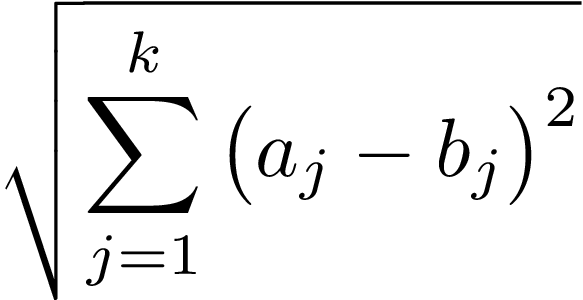
فاصله اقلیدسی همواره بزرگتر یا مساوی یک میباشد. این اندازهگیری برای نقاط یکسان برابر صفر و برای نقاطی که با هم شباهت دارند بیشتر از صفر خواهد بود. شکل زیر مثالی برای دو نقطه a و b است که هر کدام با پنج مقدار توصیف میشوند. خطچینها در شکل فواصل ![]() و
و ![]() و
و ![]() و
و ![]() و
و ![]() هستند که از معادله بالا محاسبه شدهاند.
هستند که از معادله بالا محاسبه شدهاند.
همبستگی: همبستگی پیرسون بین دو نقطه a و b با بعد k به صورت
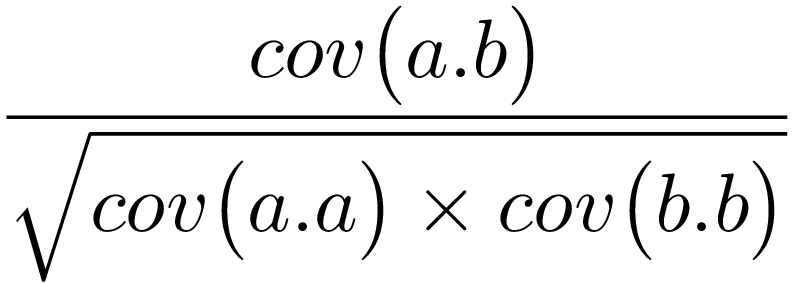
محاسبه میشود که در آن
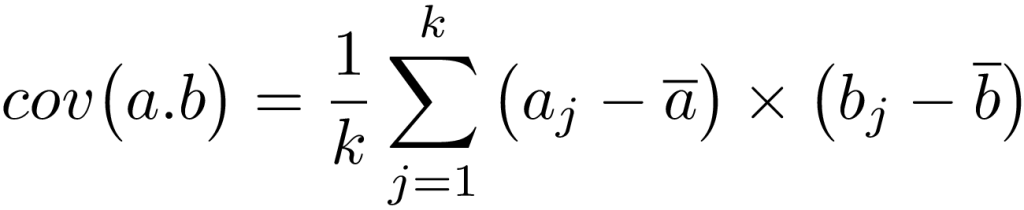
است و
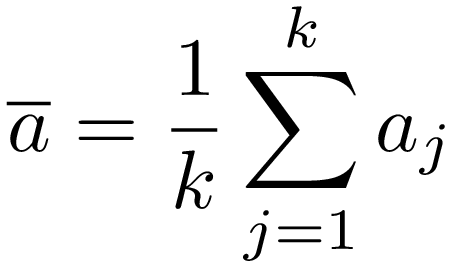
مقدار این کمیت بین 1 و 1- قرار دارد و نقاط کاملاً متفاوت همبستگی 1- و نقاط کاملا مشابه همبستگی 1 دارند. در نهایت استفاده از الگوریتم دندوگرام به ما اجازه میدهد تا بتوانیم ماتریس مجاورت را مرتب کنیم و مشاهده کنیم که آیا امکان مرتب کردن ماتریس مجاورت برای مشاهده حالت تعادل نهایی وجود دارد یا نه چرا که اگر در یک حالت مسدود قرار داشته باشیم نمیتوان ماتریس مجاورت را برای منظور فوق مرتب کرد. در شکل زیر در سمت چپ نمودار گرمایی ماتریس مجاورت و در سمت راست مرتب شده آن به وسیله الگوریتم دندوگرام و با استفاده از واحد اندازهگیری همبستگی پیرسون برای یک شبکه با 100 راس مشاهده میکنید، دینامیک شبکه دینامیک توازن بوده است.
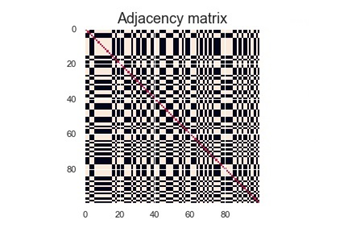
ماتریس مجاورت در حالت تعادل نهایی قبل از استفاده از الگوریتم دندوگرام 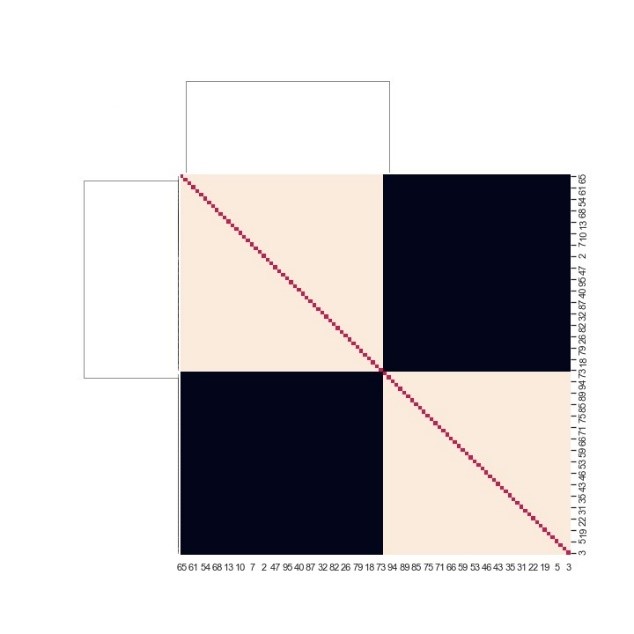
ماتریس مجاورت بعد از استفاده از الگوریتم دندوگرام که خوشهها را در آن مشاهده میکنید
آنچه در بالا گفته شد کلیات نظریه توازن و دینامیک مربوط به آن است. اگر با همین نگاه به اتفاقات جنگ جهانی اول نگاه کنیم میبینیم که تحول شبکه برهمکنشی کشورها برای رسیدن به کمترین انرژی ممکن را مشاهده میکنید[3]. در یک شبکه کامل چه از دینامیک CTD و چه از دینامیک LTD استفاده کنیم دو حالت وجود دارد که شبکه در کمترین انرژی ممکن قرار بگیرد. یکی حالتی است که اصطلاحاً به آن بهشت یا آرمانشهر میگویند، حالتی که همه دوست یکدیگر هستند و در شبکه چیزی جز مثلثهای متوازن با سه یال مثبت دیده نمیشود. حالت دیگر آن است که شبکه به دو بلوک تقسیم شود به طوری که در هر بلوک، همه دوست هم و دشمن اعضا بلوک متقابل باشند. در این حالت نیز مجدداً شبکه شامل مثلثهای متوازن است با این تفاوت که مثلثها در هر بلوک ، دارای سه یال مثبت و مثلثهای بین دو بلوک، از آنجا که دشمن مشترک دارند، دارای یک یال منفی هستند. در شکل زیر تحول شبکه جنگ جهانی اول را مشاهده میکنید.
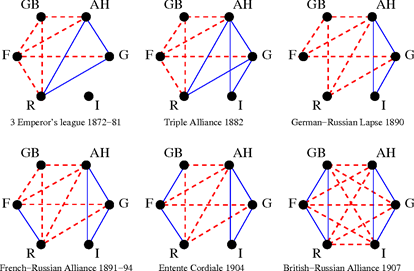
تحول روابط بین 6 کشور مهم در ماجرای جنگ جهانی اول و حرکت شبکه به سمت قرار گرفتن در انرژی کمتر. =GB بریتانیا کبیر، =AH اتریش-مجارستان، =G آلمان، =I ایتالیا، =R روسیه، =F فرانسه. در نهایت شبکه در پایدارترین حالت (کمترین انرژی) قرار گرفته است.[3]
منابع:
[1] F. Heider, The psychology of interpersonal relations. Hoboken: John Wiley & Sons Inc, 1958.
[2] S. A. Marvel, S. H. Strogatz, and J. M. Kleinberg, “Energy landscape of social balance,” Phys. Rev. Lett., vol. 103, no. 19, pp. 1–4, 2009.
[3] T. A. P. L. K. S. Redner, “Social Balance on Networks : The Dynamics of Friendship and Enmity arXiv : physics / 0605183v1 [ physics . gen-ph ] 21 May 2006,” no. February 2008, pp. 1–16.
[4] L. Hedayatifar, F. Hassanibesheli, A. H. Shirazi, and S. V. Farahani, “Pseudo paths towards minimum energy states in network dynamics,” Physica A, vol. 483, pp. 109–116, 2017.
[5] G. Jafari, A. H. Shirazi, A. Namaki, and R. Raei, “Coupled time series analysis: Methods and applications,” Comput. Sci. Eng., vol. 13, no. 6, pp. 84–89, 2011.
آخرین دیدگاهها