Unisphere

Unisphere is a simple program to evenly distribute many points on sphere. We study four different methods for distributing points on the sphere and numerically analyze their relative merits with respect to certain metrics. The analysis of the merits of the algorithms is based on the calculation of the metrics V₀ and V₁ . Given points z₁, ... , z_N on the sphere S² of unit radius we set

V_s = V_s(z₁, . . . , z_N) =

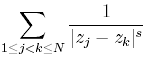
where s>0 is a positive real number and |z_j - z_k| denotes the distance in R³ of z_j and z_k . The metric V₀ = V₀ (z₁, . . . , z_N) is more appropriately defined for points on the sphere S²of unit diameter and is defined as

V₀ =

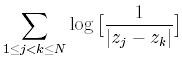
Here also |z_j - z_k| refers to the distance of z_j and z_k in R³ .

For each s≥0, the configuration of the points of minimum of V_s, demonstrates "evenly" distributed points on the sphere. For example, an equilibrium sate of N electronic charges on a sphere produces minimum Coulomb potential, V₁ . We have investigated some practical methods by which one can obtain an approximate optimal configuration of points without any explicit practice of minimization methods.

The methods are described in more detail in:

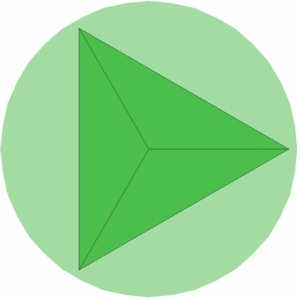
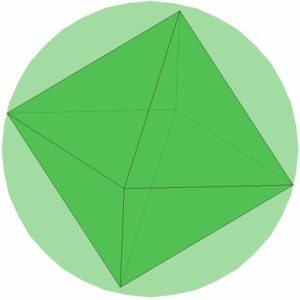
Distributing Points on the Sphere, I, Katanforoush, A., Shahshahani, M., Experimental Mathematics, 12 (2), pp. 199-209, 2003.

Optimal configuration is not necessarily fully symmetric!


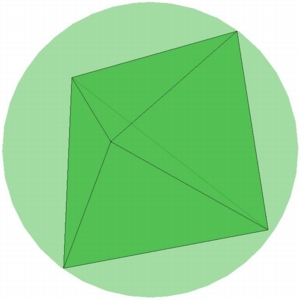
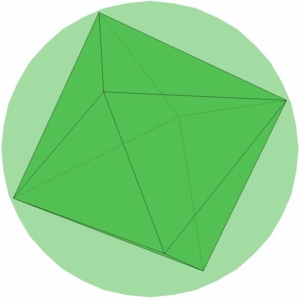
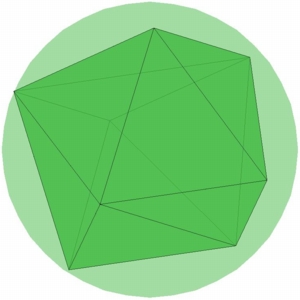
N=4, Tetrahedron	N=5	N=6, Hexahedron	N=7


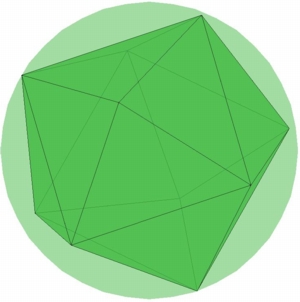
N=8, Twisted Cube	N=9	N=10	N=11


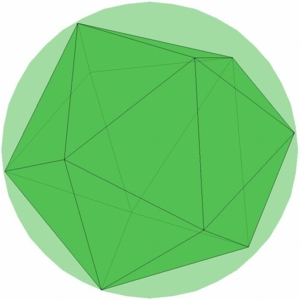
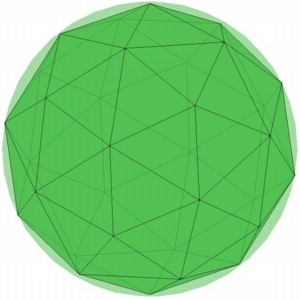
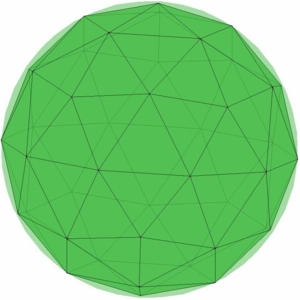
N=12, Icosahedron	N=32	N=42


N=60, Triangulated Form	N=60, Buckyball

3D data of optimal configuration of Coulomb potential in VRML format. 4.wrl, 5.wrl, 6.wrl, 7.wrl, 8.wrl, 9.wrl, 10.wrl, 11.wrl,
12.wrl, 32.wrl, 42.wrl, 60.wrl, buckyball.wrl.

Comparison of the configuration of large numbers of points

√3-Subdivision (demo2432q3s.pdf).
Starting with Lattice Points method (demo2432ls.pdf). After optimization (demo2432optls.pdf).
Starting with Polar Coordinates method (demo2432ps.pdf). After optimization (demo2432optps.pdf).

Usage

The package, Unisphere includes an instance application, SPoptim to generate points on shpere. A pre-compiled version of SPoptim is available for Win32. The simplest usage is as follows;

$ SPoptime N metric

in which N is the number of points and metric is one of three letters G|H|L. Run 'SPoptime' with no input in command shell for more info.

Optionally, the initial configuration and optimal configuration of points can be read from a text file. The output contains two coloumns of real numbers. The first coloumn denotes THETA and the second denotes PHI corresponding to spherical coordinates of each point.

Installation

The Unisphere package is written in C++. It should compile on any Unix-like system. To install the package, download the source code, unpack it, and then compile the sources, all together. This creates the SPoptim program.

[ Click here to start download ]

Contact

Ali Katanforoush, <a_katanforosh@sbu.ac.ir>, Department of Computer Science, Shahid Beheshti University, G.C., Tehran.

Time-stamp: "2010-09-18 19:47:23 katanforoush"