Drug Target Prediction

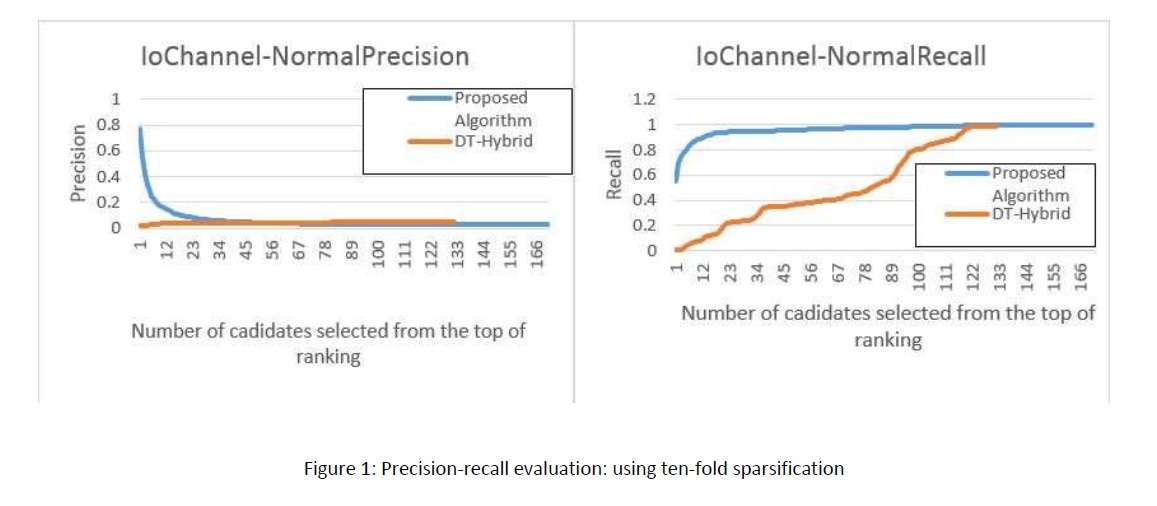
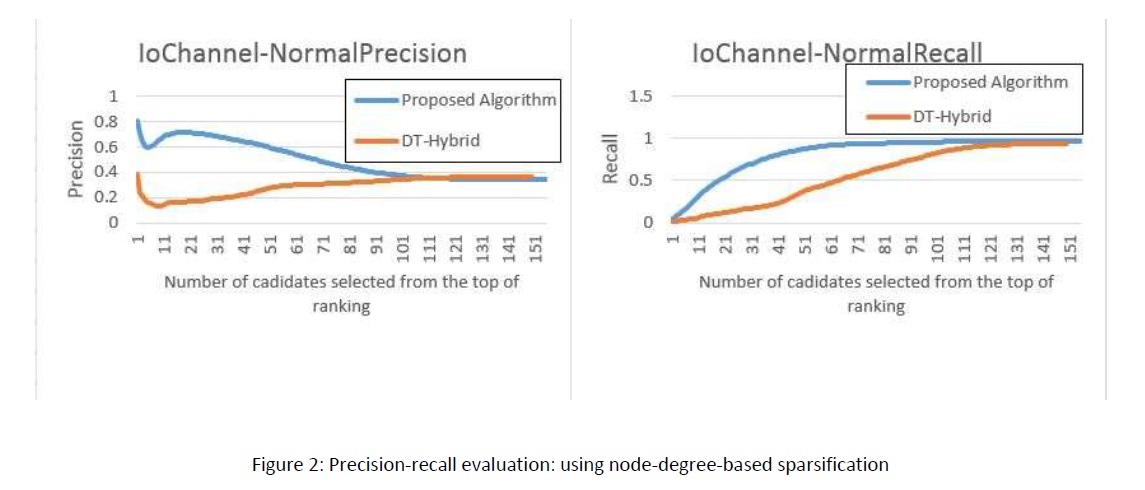
There have been a massive recent effort on the prediction of drug-target interactions for applications such as drug repurposing. New algorithms have been proposed predicting unknown interactions between existing drugs and proteins. Given an existing but incomplete adjacency matrix of binary drugtarget interactions, we wish to complete the matrix by predicting other potential interactions and turning as much zeros as possible to ones. This will result in a denser matrix containing more information. Different approaches have been taken, from machine learning methods to probabilistic modeling. Among the literature, the nearest work to ours is DT-Hybrid algorithm which constructs a score matrix for each drug and candidates proteins with highest scores to interact with the selected drug. We propose a new algorithm to boost both the performance and efficiency of DT-Hybrid, by elaborating a different metric for constructing the score matrix. We show the superiority of our method compared to DT-Hybrid, both in terms of accuracy and computational complexity. We used Drugbank datasets Enzymes, Ion Channels, GPCRs and Nuclear Receptors as our evaluation sets. We are also planning to evaluate this work on the full Drugbank database with up to 4000 drugs and 6000 proteins. We computed inter-drug and inter-protein similarities using and. For evaluating our method, we first sparsify the matrix with two different approaches and try to reconstruct the missing interactions by the proposed algorithm. Then we compute precision and recall measures to compare it with that of our baseline. Figure 1 and 2 illustrate our results on Enzyme dataset, for each of the two sparsifying approaches. In Figure 1 (ten-fold), we sparsify the matrix by omitting ten percent of the interactions, maintaining the connectedness of the drug-target graph. In Figure 2 (node-degree), we find the highest degree that can be subtracted from every node, again maintaining the connectedness of the graph. Both figures denote significant improvement of the stateof-the-art by our method.

For computational complexity analysis, we demonstrate the runtime of the proposed methods, on different datasets. We include the runtime in case of both sparsifying methods.

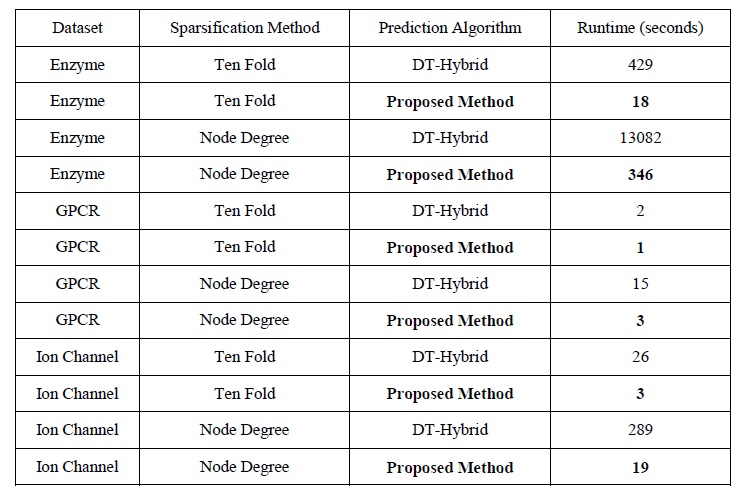
The significant superiority of the proposed method is due to the computational complexity of O(n2) compared to O(n4) for DT-Hybrid.